728x90
[백준] 연속합 (1912번 JAVA) (!) / 400 - 다이나믹 프로그래밍 1
[접근 방법]
문제 고민에 굉장히 많은 시간을 소요하였다.
"DP 문제는 모든 것을 내가 구현할 필요는 없다."
라는 것을 다시끔 일깨워 준 문제 였다.
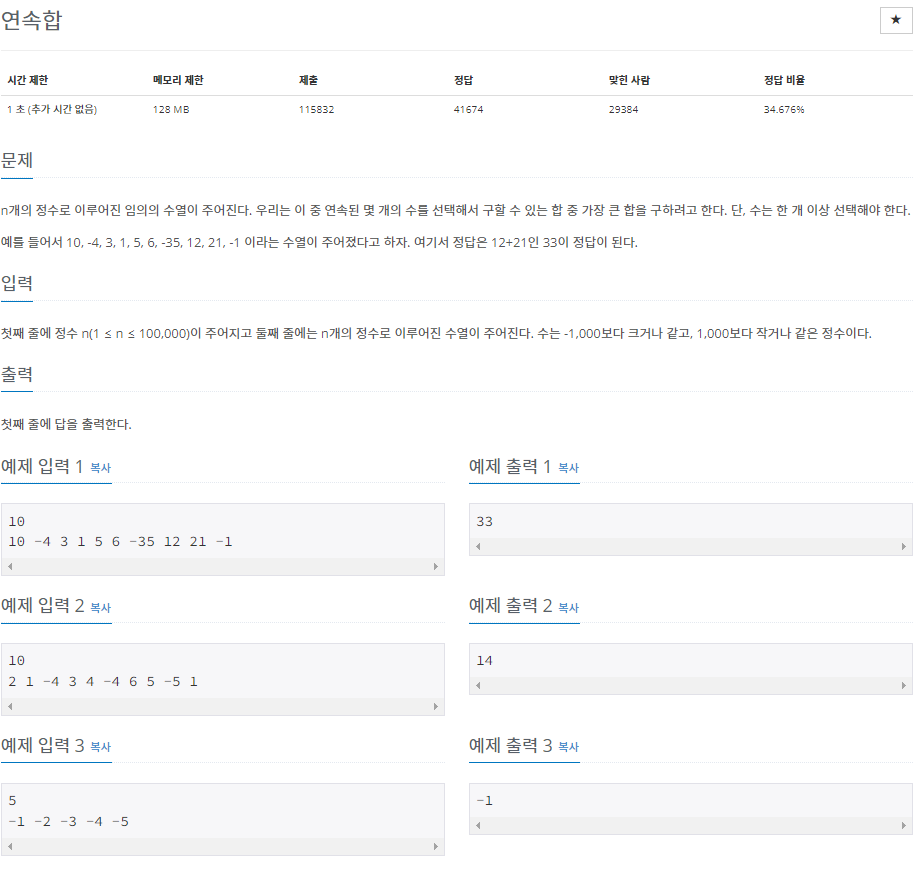
즉, 예제 1번 처럼
[10, -4, -3, 1, 5, 6, -35, 12, 21, -1] 이 주어지는 경우
직접 프로그래밍으로 어느 지점의 연속된 수의 합이 최대값 인지를 구할 필요가 없다는 것이다.
'음수가 나오는 경우' , '음수 뒤에 양수가 나와서, 둘다 더하는 것이 이득인지 아닌지' 등 복잡한 경우들을 직접 고려하여 해결할 필요는 없는 것이다.
그냥 방법만 알려주고, 놓고 온다는 표현이 적절할 것 같다.
for(int i=1; i<n; i++){
DP[i] = Math.max(DP[i-1] + arr[i], arr[i]);
max = Math.max(DP[i], max);
}DP[i] = Math.max(DP[i-1] + arr[i], arr[i])
위 코드와 같이 이전 연속합에 잇는 것이 더 큰지, 잇지 않고 새로운 연속합을 생성하는 것이 더 큰지를 비교하여 최대값을 도출한다.
[JAVA 코드]
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.*;
public class Main{
public static int[] arr;
public static int[] DP;
public static int max;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 1 <= n <= 100_000
int n = Integer.parseInt(br.readLine());
DP = new int[n];
arr = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
DP[0] = arr[0];
max = DP[0];
for(int i=1; i<n; i++){
DP[i] = Math.max(DP[i-1] + arr[i], arr[i]);
max = Math.max(DP[i], max);
}
bw.write(max + "\n");
bw.flush();
bw.close();
}
}import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.*;
public class Main{
public static int[] arr;
public static Integer[] DP;
public static int max;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 1 <= n <= 100_000
int n = Integer.parseInt(br.readLine());
DP = new Integer[n];
arr = new int[n];
StringTokenizer st = new StringTokenizer(br.readLine());
for(int i=0; i<n; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
DP[0] = arr[0];
max = DP[0];
recur(n - 1);
bw.write(max + "\n");
bw.flush();
bw.close();
}
public static int recur(int N){
if (DP[N] == null){
DP[N] = Math.max(recur(N-1) + arr[N], arr[N]);
max = Math.max(DP[N], max);
}
return DP[N];
}
}728x90
'백준 > DP' 카테고리의 다른 글
| [백준] 합분해 (2225번 JAVA) (!) / 400 - 다이나믹 프로그래밍 1 (0) | 2023.01.17 |
|---|---|
| [백준] 제곱수의 합(1699번 JAVA) (!) / 400 - 다이나믹 프로그래밍 1 (1) | 2023.01.16 |
| [백준] 가장 긴 증가하는 부분 수열 4 (14002번 JAVA) / 400 - 다이나믹 프로그래밍 1 (0) | 2023.01.16 |
| [백준] 가장 긴 증가하는 부분 수열 (!) (11053번 JAVA) / 400 - 다이나믹 프로그래밍 1 (2) | 2023.01.15 |
| [백준] 다이나믹 프로그래밍(DP) - "1, 2, 3 더하기" 시리즈 (1) | 2023.01.15 |
