[programmers] 합승 택시 요금 (JAVA)

[ 2021 KAKAO BLIND RECRUITMENT - 합승 택시 요금 ]

https://school.programmers.co.kr/learn/courses/30/lessons/72413

프로그래머스

 

[ 접근 방법 ]

최소 금액(Cost)을 구하는 문제이다.

다익스트라 알고리즘을 사용하여 문제를 해결하였다.

 

기존 다익스트라 알고리즘 문제에서 '합승' 이라는 새로운 조건이 추가 되었다.

이 부분은

- '시작점' ~ '합승 목적지' (StartToK)

- 'A 목적지' ~ '합승 목적지' (AToK)

- 'B 목적지' ~ '합승 목적지' (BToK)

이렇게 3가지로 나눠, 세 값의 합의 최솟값을 구하는 방식을 이용했다.

 

1. 목적지(노드) 사이 비용 2차원 배열에 입력하기

 

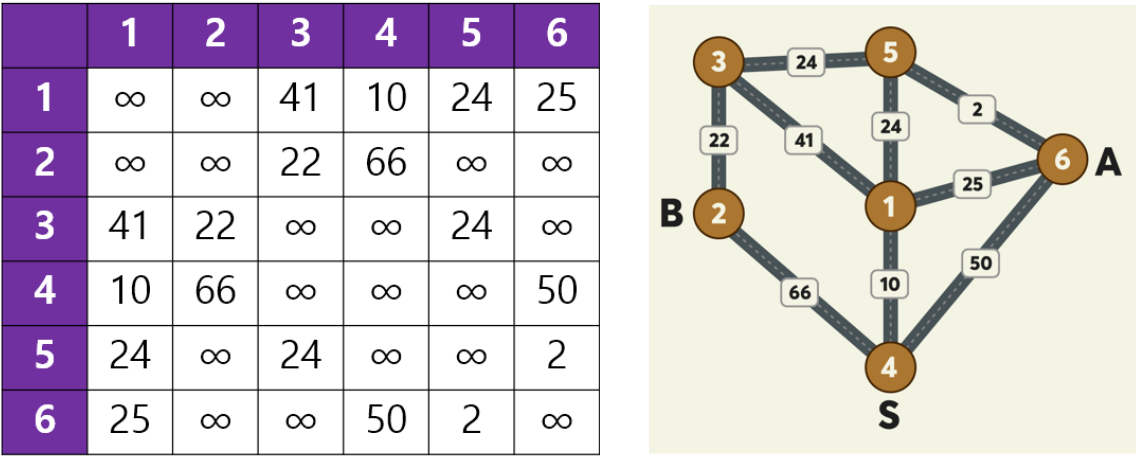
2. 다익스트라 알고리즘 구현하기

  static int[][] prices; //노드 사이 이동 비용
  
  //다익스트라 알고리즘
  private int[] dijkstra (int n, int start) {
    int[] result = new int[n+1];
    boolean[] visited = new boolean[n+1];

    Arrays.fill(result, Integer.MAX_VALUE);
    result[start] = 0;
    visited[start] = true;

    for(int i = 1; i <= n; i++) {
      if (!visited[i] && prices[start][i] != Integer.MAX_VALUE) {
        result[i] = prices[start][i];
      }
    }

    //최소 거리 노드 찾기
    for (int i = 1; i < n; i++) {

      int min = Integer.MAX_VALUE;
      int min_index = -1;

      // 탐색 안한 노드 중에 현재 최소 거리 노드 => 앞으로 탐색할 노드
      for (int j = 1; j <= n; j++) {
        if (!visited[j]) {
          if (result[j] < min) {
            min = result[j];
            min_index = j;
          }
        }
      }

      if (min_index == -1) {
        break;
    }

      // 거쳐가는것과 비교해 최솟값 갱신
      visited[min_index] = true;
      for (int j = 1; j <= n; j++) {
        if (!visited[j] && prices[min_index][j] != Integer.MAX_VALUE) {
          if (result[min_index] + prices[min_index][j] < result[j]) {
            result[j] = result[min_index] + prices[min_index][j];
          }
        }
      }

    }

    return result;
  }

 

3. 세 거리 합의 최솟값 구하기

- '시작점' ~ '합승 목적지' (StartToK)

- 'A 목적지' ~ '합승 목적지' (AToK)

- 'B 목적지' ~ '합승 목적지' (BToK)

 

[ JAVA 코드 ]

import java.util.*;

class PM_72413 {

  static int[][] prices;

  public int solution(int n, int s, int a, int b, int[][] fares) {

    prices = new int[n+1][n+1];
    for (int[] arr : prices) {
      Arrays.fill(arr, Integer.MAX_VALUE);
    }
    for (int[] f : fares) {
      int dot1 = f[0];
      int dot2 = f[1];
      int price = f[2];

      prices[dot1][dot2] = price;
      prices[dot2][dot1] = price;
    }

    int[] fromS = dijkstra(n, s);
    int[] fromA = dijkstra(n, a);
    int[] fromB = dijkstra(n, b);
    
    int min_price = Integer.MAX_VALUE;
    for (int i = 1; i <= n; i++) {
      if (fromS[i] != Integer.MAX_VALUE && 
          fromA[i] != Integer.MAX_VALUE && 
          fromB[i] != Integer.MAX_VALUE ) {
        
            min_price = Math.min(min_price, fromS[i] + fromA[i] + fromB[i]);
      }
    }

    return min_price;
  }



  //다익스트라 알고리즘
  private int[] dijkstra (int n, int start) {
    int[] result = new int[n+1];
    boolean[] visited = new boolean[n+1];

    Arrays.fill(result, Integer.MAX_VALUE);
    result[start] = 0;
    visited[start] = true;

    for(int i = 1; i <= n; i++) {
      if (!visited[i] && prices[start][i] != Integer.MAX_VALUE) {
        result[i] = prices[start][i];
      }
    }

    //최소 거리 노드 찾기
    for (int i = 1; i < n; i++) {

      int min = Integer.MAX_VALUE;
      int min_index = -1;

      // 탐색 안한 노드 중에 현재 최소 거리 노드 => 앞으로 탐색할 노드
      for (int j = 1; j <= n; j++) {
        if (!visited[j]) {
          if (result[j] < min) {
            min = result[j];
            min_index = j;
          }
        }
      }

      if (min_index == -1) {
        break;
    }

      // 거쳐가는것과 비교해 최솟값 갱신
      visited[min_index] = true;
      for (int j = 1; j <= n; j++) {
        if (!visited[j] && prices[min_index][j] != Integer.MAX_VALUE) {
          if (result[min_index] + prices[min_index][j] < result[j]) {
            result[j] = result[min_index] + prices[min_index][j];
          }
        }
      }

    }

    return result;
  }
}

 

[ 발전 방향 ]

 

유명 알고리즘에 대한 숙지가 필요하다.

유명 알고리즘을 기반으로 변형 문제에 대한 대비가 필요하다.