[백준] 1, 2, 3 더하기 (★) (9095번 JAVA) / 400 - 다이나믹 프로그래밍 1
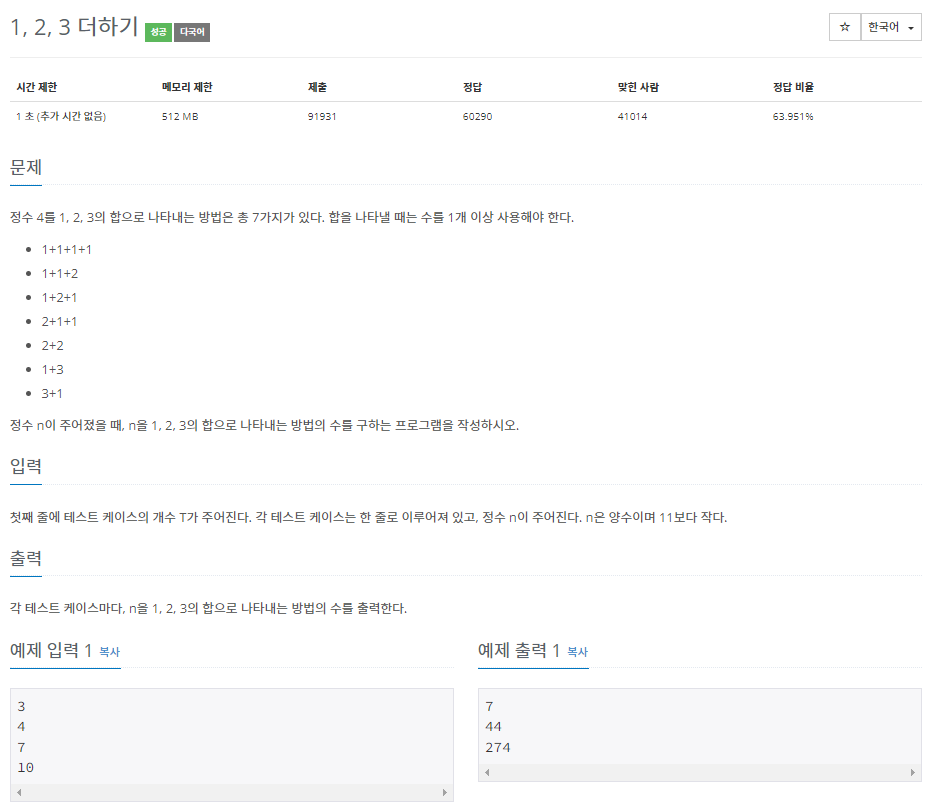
[접근 방법]
1을 나타내는 방법 : 1가지 {1}
2를 나타내는 방법 : 2가지 {2} , {1,1}
3을 나타내는 방법 : 4가지 {3} , {2, 1}, {1, 2}, {1, 1, 1}
위 3가지를 전제조건으로 한다.
4의 합을 나타내는 순서쌍은 (1,3) , (2,2) , (3,1) 과 같이 나타낼 수 있다.
(1,3) 은 (1을 더하는 방법 : 1가지) * (3을 나타내는 방법 : 4가지) => 4
(2,2) 은 (2를 더하는 방법 : 1가지) * (2를 나타내는 방법 : 2가지) => 2
(3,1) 은 (3을 더하는 방법 : 1가지) * (1을 나타내는 방법 : 1가지) => 1
4를 나타내는 방법 : 4 + 2 + 1 = 7가지
여기서 주의할 점은 "3을 더하는 방법" != "3을 나타내는 방법" 이라는 것이다.
3을 더하는 방법은 말그대로 3을 더하는 행위일 뿐이다.
5를 나타내는 방법으로 다시 한번 예를 들겠다.
5의 합을 나타내는 순서쌍은 (1,4) , (2,3) , (3,2) 과 같이 나타낼 수 있다.
(1,4) 은 (1을 더하는 방법 : 1가지) * (4을 나타내는 방법 : 7가지) => 7
(2,3) 은 (2를 더하는 방법 : 1가지) * (3를 나타내는 방법 : 4가지) => 4
(3,2) 은 (3을 더하는 방법 : 1가지) * (2을 나타내는 방법 : 2가지) => 2
5를 나타내는 방법 : 7 + 4 + 2 = 13가지
따라서,
dp[N] = dp[N-1] + dp[N-2] + dp[N-3]의 점화식을 만들 수 있다.
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class Main{
public static Integer[] dp;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 1 ~ 10
dp = new Integer[11];
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
recur(10);
int T = Integer.parseInt(br.readLine());
for(int i=0; i<T; i++){
int N = Integer.parseInt(br.readLine());
bw.write(dp[N] + "\n");
}
bw.flush();
bw.close();
}
public static int recur(int N){
if (dp[N] == null){
dp[N] = recur(N - 1) + recur(N - 2) + recur(N - 3);
}
return dp[N];
} // recur
}[ 2회차 풀이 (1/28) ]
[접근 방법]
접근 방법은 1회차 풀이와 같다.
실행 시간 : 1초 = 약 2000만번 연산
N의 범위 (1<=N<=11)
=> 시간 복잡도에 대한 별다른 고려 필요 없음
[JAVA 코드]
// 9095 - 1, 2, 3 더하기
import java.util.*;
import java.io.*;
class Main {
public static void main(String[] args) throws IOException {
// 0. 입출력 선언 / 초기화
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int T = Integer.parseInt(br.readLine());
int[] DP = new int[12];
DP[1] = 1; // 1
DP[2] = 2; // 1+1, 2
DP[3] = 4; // 1+1+1, 1+2, 2+1, 3
/*
* DP[N] = DP[N-1] + DP[N-2] + DP[N-3]
* N-1 을 구성하는 방법 = N-1을 구성하고 +1 을 하여 N을 구성하는 방법
* N-2 을 구성하는 방법 = N-2을 구성하고 +2 을 하여 N을 구성하는 방법
* N-3 을 구성하는 방법 = N-3을 구성하고 +3 을 하여 N을 구성하는 방법
*
* 따라서, N을 구성하는 방법
* = N-1을 구성하는 방법 + N-2를 구성하는 방법 + N-3을 구성하는 방법
*/
for(int i = 4; i<=11; i++){
DP[i] = DP[i-1] + DP[i-2] + DP[i-3];
}
for(int i=0; i<T; i++){
int n = Integer.parseInt(br.readLine());
bw.write(DP[n] + "\n");
}
bw.flush();
bw.close();
br.close();
}
}
/*
* 실행 시간 1초 = 약 2000만번 연산
*
* N의 범위 (1 <= N <= 11)
* 시간복잡도에 대한 별다른 고려 필요 없음
*/[Rewind]
1. 어려웠던 점
-
2. 알게된 점
- 두번째 풀게되어 점화식을 쉽게 찾았다.
3. 해결방안
-
'백준 > DP' 카테고리의 다른 글
| [백준] 1, 2, 3 더하기 2 (!) (12101번 JAVA) (0) | 2023.01.14 |
|---|---|
| [백준] 1, 2, 3 더하기 5 (★) (15990번 JAVA) / 400 - 다이나믹 프로그래밍 1 (1) | 2023.01.13 |
| [백준] 카드 구매하기 2 (16194번 JAVA) / 400 - 다이나믹 프로그래밍 1 (1) | 2023.01.13 |
| [백준] 카드 구매하기 (★) (11052번 JAVA) / 400 - 다이나믹 프로그래밍 1 (0) | 2023.01.13 |
| [백준] 1로 만들기 (★) (1463번 JAVA) / 400 - 다이나믹 프로그래밍 1 (0) | 2023.01.11 |
