1. Dynamic Programming (동적 계획법) 이란?
: 큰 문제의 해답에 작은 문제의 해답이 포함되어 있고, 이를 재귀호출 알고리즘으로 구현하면 지나친 중복이 발생하는 경우에 이 재귀적 중복을 해결하는 방법을 뜻한다.
=> 주어진 문제를 풀기 위해서, 문제를 여러 하위 문제로 나누어 해결한 다음 그 해결책을 저장해 둔 후 결합하여 주어진 문제를 해결하는 문제해결 패러다임이라고 할 수 있다.
* 최적 부분 구조를 이룬다. (Optimal Substructure)
* 재귀적으로 구현했을 때 중복 호출로 심각한 비효율이 발생한다. (Overlapping Recursive Call)
위 두가지 성질이 있는 문제에 대해 적절한 저장 방법으로 중복 호출의 비효율을 제거한 것을 "동적 계획법" 이라 한다.
최적 부분 구조 (Optimal Substructure) 란?
: 상위 문제의 해답에 하위 문제의 해답이 포함되어 있는 것
EX ) 피보나치 수열 : fib(n) = fib(n-1) + fib(n-2)
이 피보나치 수열을 재귀적으로 호출 하였을 때, 어떠한 문제가 있는가?
fib(5)를 재귀 호출 방식으로 해결한다면,
fib(5) = fib(4) + fib(3)
fib(4) = fib(3) + fib(2)
fib(3) = fib(2) + fib(1) 와 같은 방식으로 하향식 으로 문제를 해결하기 때문에,
fib(5)를 구하기 위해서 [fib(4) ; 1번] , [fib(3) ; 2번] , [fib(2) ; 3번] , [fib(1) ; 2번] 호출이 된다.
같은 문제를 여러번 호출하게 되는 중복 호출이 발생하게 된다.
fib(5)를 예로들어, 그다지 많은 호출 같지 않아 보일 수 도 있다. 그러나 값이 커질수록 기하급수적으로 부하를 미친다.
피보나치 수열을 재귀 호출로 구현
// 피보나치 수열 (재귀 호출 방식)
#include <stdio.h>
int fibonacci(int n)
{
if(n == 1 || n==2){
return 1;
}
else{
return fibonacci(n-1) + fibonacci(n-2);
}
}
int main()
{
printf("%d", fibonacci(12));
return 0;
}
/*
144
*/재귀 호출로 구현한 피보나치 수열의 시간복잡도 : O(2**n)
피보나치 수열을 DP로 구현
// 피보나치 수열 동적 계획법
#include <stdio.h>
int f[100] = {0};
int fibonacci(int n)
{
if(f[n] != 0){
return f[n];
}
else{
if (n==1 || n==2){
f[n] = 1;
}
else {
f[n] = fibonacci(n-1) + fibonacci(n-2);
}
return f[n];
}
}
int main()
{
int A = fibonacci(12);
printf("%d \n", A);
}
/*
144
*/DP로 구현한 피보나치 수열의 시간복잡도 : O(n)
1-Q1. Dynamic Programming (동적 계획법)과 Divide and Conquer (분할 정복)은 뭐가 다른가?
DP의 정의를 보고나서 "분할 정복" 방법이 가장 먼저 떠오르게 되었다.
DP와 분할 정복은 "주어진 문제를 해결하기 위해, 문제를 여러 하위 문제로 분할 하여 해결" 하는 것이라는 공통의 개념을 가지고 있다.
그렇다면 이 둘의 차이점은 무엇인가?
DP는 주어진 문제를 해결하기 위해, 여러 하위 문제들로 나눈 뒤, 하위 문제들의 해를 활용하여 상위 문제를 해결한다.
이때, 하위 문제들은 중복되어 발생 하므로, 하위 문제를 해결한 방법을 저장해 두었다가, "같은 하위문제가 발생한다면, 저장해두었던 값을 다시 사용한다." => Memoization 기법 (한번만 계산해 두면 다시 계산할 필요가 없음)
Memoization 기법 : 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기법
DP는 상향식 접근법으로, 가장 최하위 문제의 해답을 구한 후, 이를 저장하고 이 결과값을 바탕으로 상위 문제를 해결한다.
DP로 해결하기 적절한 문제는 재귀적으로 구현했을 때 중복 호출로 심각한 비효율이 발생 할때 이다.
즉, 같은 하위 문제가 많이 발생하는 경우이다. EX) 피보나치 , LCS
분할 정복 기법 은 주어진 문제를 해결하기 위해, 문제를 나눌 수 없을 때까지 나눈후 이를 해결하고 병합하여 문제의 답을 얻는 방법이다.
하향식 접근법으로, 상위의 답을 구하기 위해, 아래로 내려가면서 하위의 답을 구하는 방식이다.
분할 정복 기법으로 해결하기 적절한 문제는 문제를 분할하였을때 하위 문제가 서로 중복되지 않는 문제이다.
EX) 병합 정렬, 퀵 정렬
즉, DP => 하위 문제가 중복 => 메모이제이션 기법을 사용해서 부하를 줄임
분할정복 => 하위 문제가 중복되지 않음 => 단지 하위 문제 해결 후 병합 => 상위 문제 해결
* Dynamic Programming 의 예시
막대 자르기 문제 (Rod Cutting Problem)
문제
[길이가 n인 막대와 i = 1,2,3, ... ,n에 대한 가격 p_i의 표가 주어지고 해당 막대를 판매하였을때 얻을 수 있는 최대 수익 r_n을 결정하는 것.
단, 길이가 n인 막대의 가격 p_n이 가장 비싼 값이 된다면, 굳이 막대를 자르지 않아도 된다.]

예시 ) 막대의 길이가 4인 경우

순서대로 각 경우의 최적해는
(a) : 9
(b) : 1+8 = 9
(c) : 5+5 = 10
(d) : 8+1 = 9
(e) : 1+1+5 = 7
(f) : 1+5+1 = 7
(g) : 5+1+1 = 7
(h) : 1+1+1+1 = 4
이므로, 길이가 4인 막대를 자르는 모든 경우를 고려해 보았을때, 해당 막대를 판매하였을때 얻을 수 있는 최대 수익은 (c)의 경우인 10이다.
이 막대 자르기 문제의 재귀 호출 의사코드이다.
// 재귀 호출 의사코드
CutRod (p,n)
if n == 0
return 0
q = -무한대
for i = 1 to n
q = max(q,p[i] + CutRod(p,n-i))
return q위와 같이 재귀호출 방식으로 문제를 해결한다면,
i가 1 부터 n까지의 모든 경우에 대해, 재귀적으로 함수를 호출하고, 한번 계산 하였던 값을 반복적으로 계산하기 때문에 비효율적이다.
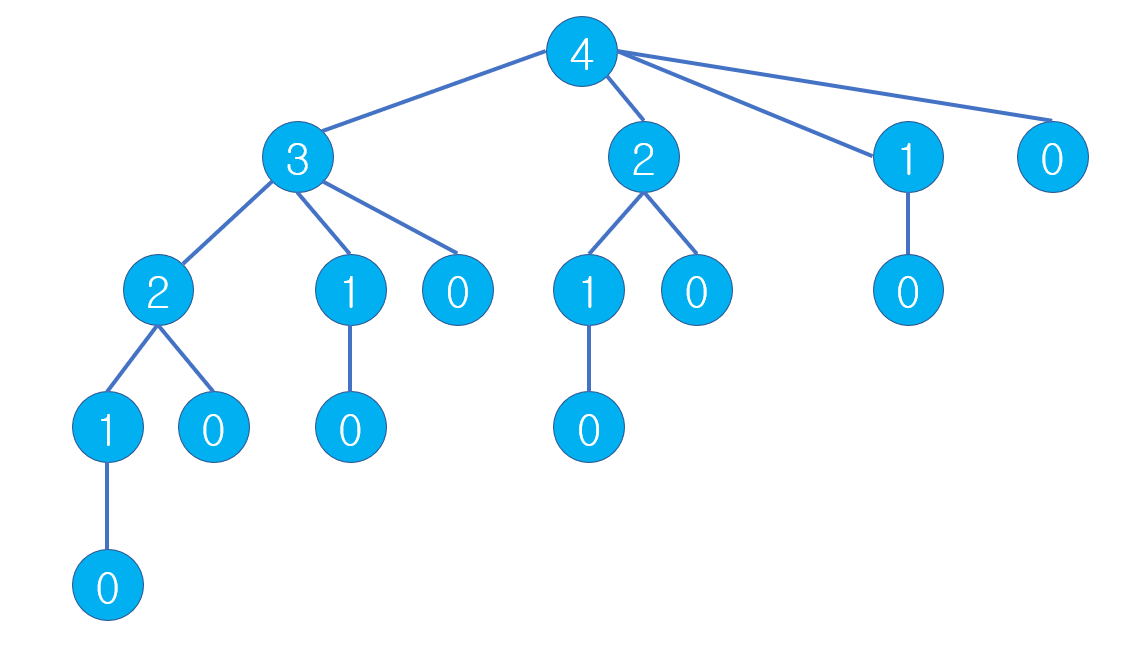
위와 같이 길이가 4인 막대인 경우, 길이가 1인 경우 4번, 2인 경우 2번 등 같은 연산을 반복하여 해결하는 것을 볼 수 있다.
따라서 길이가 n인 막대를 자르는 모든 경우의 수인 2**(n-1)번을 모두 계산하므로, 재귀호출 방식의 시간 복잡도는 지수함수에 수렴한다.
이와 같이 "최적 부분 구조"를 이루고, "재귀 방식으로 해결하였을 때, 중복 호출로 엄청난 비효율이 발생"하므로, DP 방식을 이용하여 해결하여야 한다.
DP 재귀 호출 의사코드이다.
// DP 의사코드
DP-Cut-Rod(p, n)
let r[0 .. n] be a new array
r[0] = 0
for j = 1 to n
q = -무한대
for i = 1 to j
q = max(q, p[i] + r[j - i])
r[j] = q
return r[n]배열 r[]의 구조는 길이가 n' (n >= n')인 막대의 최적해를 r[n']에 저장된 구조이다.
이를 통해 같은 연산을 반복하지 않고 r[]에 저장된 값을 이용한다.
이러한 상향식 접근법의 DP방식의 시간복잡도는 평균적으로 n**2에 수렴한다.
이와 같은 최적 부분 구조를 이루고, 재귀적으로 구현했을 때 중복 호출로 심각한 비효율이 발생하는 문제에 대해서는 재귀 호출 방식으로 해결하는 것 보다 동적 계획법으로 해결하는 것이 더 효율적임을 알 수 있다.
아래는 재귀호출 방식, 동적 계획법 의 C언어 코드이다.
재귀호출 방식
// 막대 자르기 (재귀 호출)
#include <stdio.h>
#define _CRT_SECURE_NO_WARNINGS
#define Arr_Size 100
int find_max(int p_r, int n_r){
if (p_r > n_r){
return p_r;
}
return n_r;
}
int CutRod (int *p, int n){
int q;
if (n == 0){
return 0;
}
q = -1; // q 초기화
for (int i=1; i<n+1; i++){ // i : 1 ~ n
q = find_max(q, p[i] + CutRod(p, n-i));
}
return q;
}
int main()
{
int price[Arr_Size] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
printf("Rod Length : ");
int Rod_Length;
scanf("%d", &Rod_Length);
printf("price : ");
for (int i = 1; i < Rod_Length+1 ; i++)
printf(" %d |", price[i]);
int result = CutRod(price, Rod_Length);
printf("Best Price (Recursive Call) : %d ", result);
return 0;
}실행 결과

동적 계획법
// Botton - Up DP
#include <stdio.h>
#define _CRT_SECURE_NO_WARNINGS
#define Arr_Size 100
int max(int p_r, int n_r) {
if(p_r > n_r) return p_r;
return n_r;
}
int Cut_Rod(int *p, int n)
{
int q;
int r[Arr_Size] = {0,};
r[0] = 0;
for(int j = 1; j < n+1; j++){
q = -1;
for(int i = 1; i < j+1; i++){
q = max(q, p[i] + r[j - i]);
}
r[j] = q;
}
return r[n];
}
int main()
{
int price[Arr_Size] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
printf("Rod Length : ");
int Rod_Length;
scanf("%d", &Rod_Length);
printf("\nprice : ");
for (int i = 1; i < Rod_Length+1 ; i++)
printf(" %d |", price[i]);
int result = Cut_Rod(price, Rod_Length);
printf("Best Price (DP) : %d ", result);
return 0;
}실행 결과

'Algorithm' 카테고리의 다른 글
| 깊이/너비 우선탐색 (DFS / BFS) 알고리즘 / Java 코드 (0) | 2024.08.08 |
|---|---|
| [알고리즘] 다익스트라(Dijkstra) 알고리즘 + Java 코드 (0) | 2024.07.31 |
| "탐색 (Search)" 알고리즘에 대해 알아보자. (0) | 2023.02.03 |
