- 개요
다익스트라 알고리즘은 '그래프의 한 정점에서 모든 정점까지의 최단 거리를 각각 구하는 알고리즘' 이다.
(최단 경로 문제 | Shortest Path Problem)
시작점 부터 순차적으로 최단 거리를 구하는 방식으로 진행된다.
- 예시를 이용한 알고리즘 설명
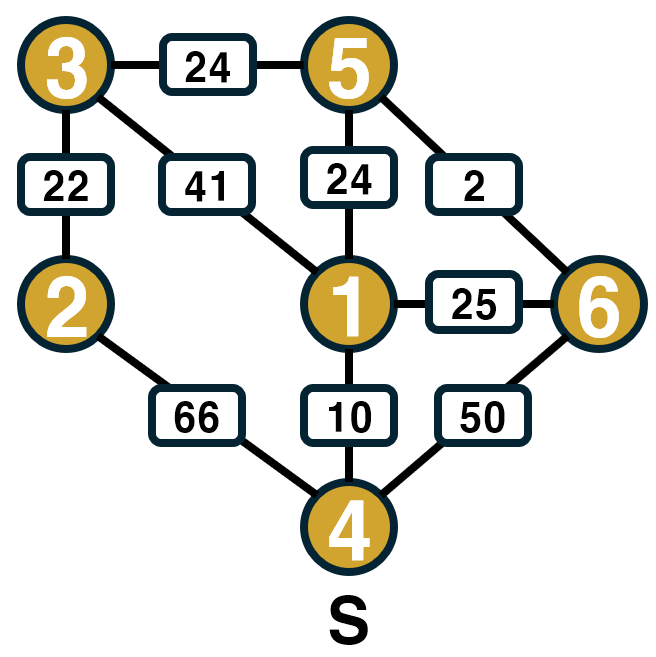
위와 같은 경로맵이 있다.
시작점은 "정점 4" 이다.

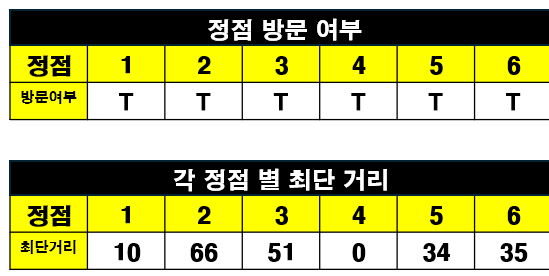
'정점 방문 여부' 와 '각 정점 별 최단 거리' 테이블을 통해 순차적으로 최단 거리를 구한다.
시작점인 '정점 4' 는 이미 방문한 것으로 표시하고, 시작점이기 때문에 최단 거리는 0 으로 설정한다.
[탐색 정점 : 정점 4]
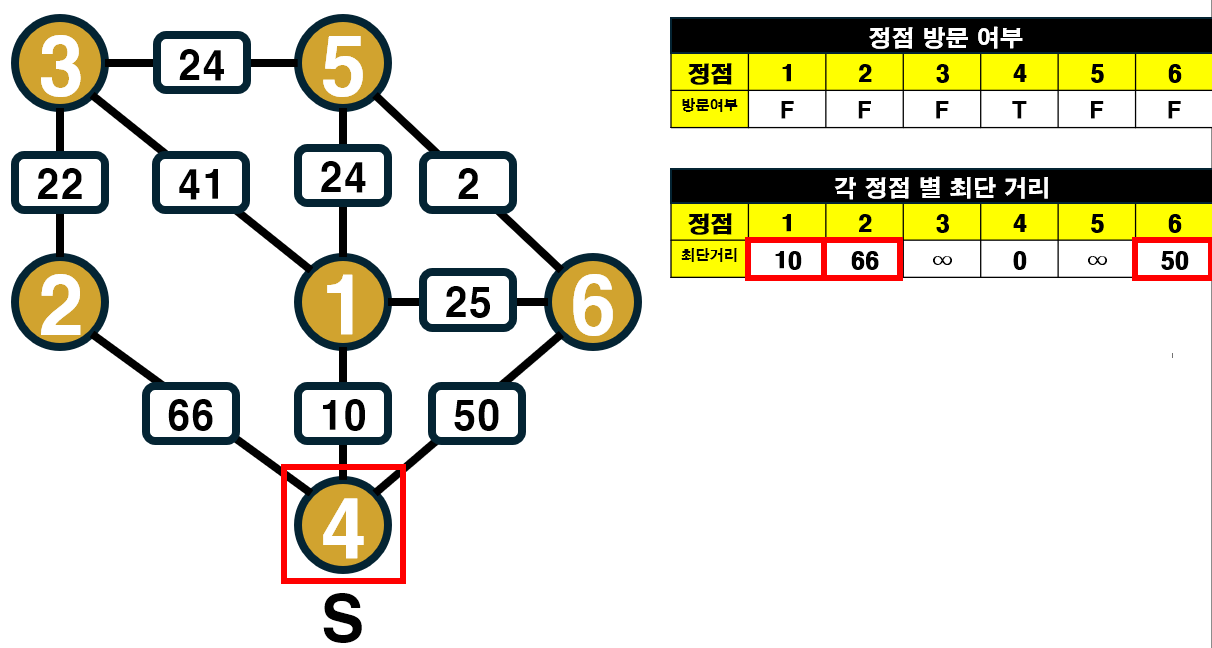
정점 4 와 인접한 정점 2, 1, 6 에 대해 최단 거리를 갱신한다.
[탐색 정점 : 정점 1]
미방문 상태인 정점 (1, 2, 3, 5, 6) 중 출발점으로 부터 가장 짧은 거리를 가지고 있는 정점 => 정점 1
정점 1을 기준으로 인접한 정점을 탐색한다.
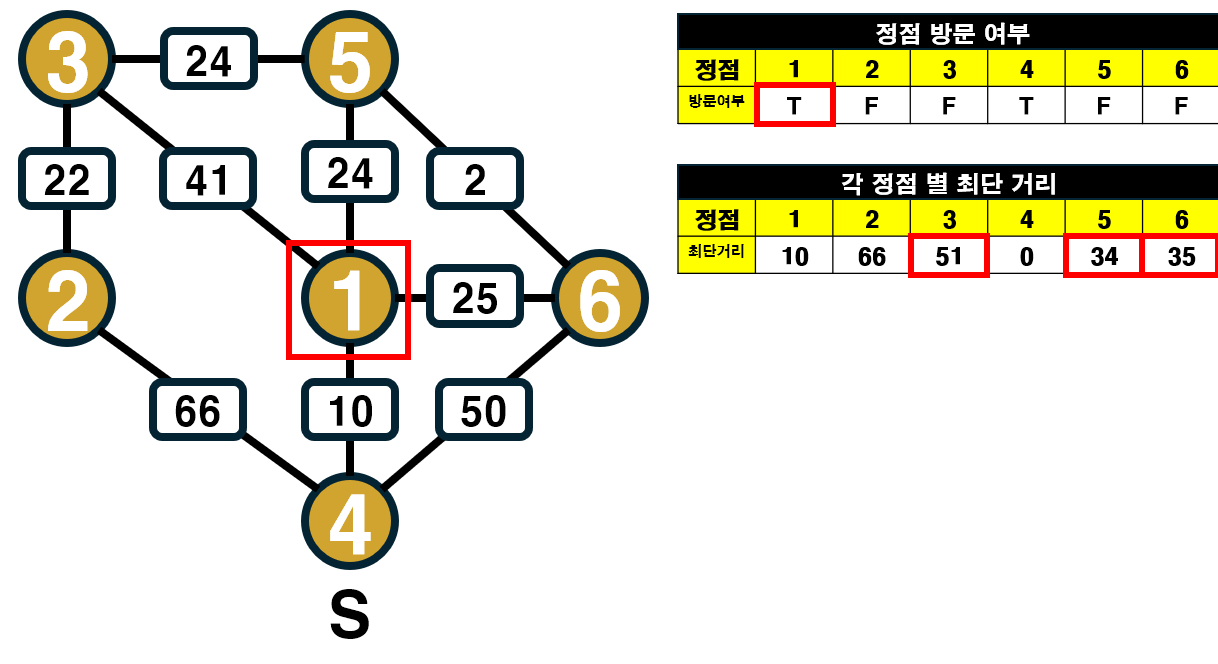
정점 1과 인접한 정점 3, 5, 6 까지의 거리를 구하고 기존과 비교하여, 최단 거리를 갱신한다.
정점 3 최단 거리 : 기존 거리 (∞) > 새로운 거리 (10 + 41 = 51) 이므로, 새로운 거리가 최단 거리로 갱신된다.
※ 출발점 부터 정점 1까지의 최단 거리가 10 이므로 10을 더해준다.
정점 5 최단 거리 : 기존 거리 (∞) > 새로운 거리 (10 + 24 = 34) 이므로, 새로운 거리가 최단 거리로 갱신된다.
정점 6 최단 거리 : 기존 거리 (50) > 새로운 거리 (10 + 25 = 35) 이므로, 새로운 거리가 최단 거리로 갱신된다.
정점 1을 탐색 했음으로 방문표시를 한다.
[탐색 정점 : 정점 5]
미방문 상태인 정점 (2, 3, 5, 6) 중 출발점으로 부터 가장 짧은 거리를 가지고 있는 정점 => 정점 5
정점 5을 기준으로 인접한 정점을 탐색한다.

정점 5과 인접한 정점 3, 6 까지의 거리를 구하고 기존과 비교하여, 최단 거리를 갱신한다.
정점 3 최단 거리 : 기존 거리 (51) > 새로운 거리 (34 + 24 = 58) 이므로, 최단 거리가 기존 거리로 유지된다.
정점 6 최단 거리 : 기존 거리 (35) > 새로운 거리 (34 + 2 = 36) 이므로, 최단 거리가 기존 거리로 유지된다.
정점 5을 탐색 했음으로 방문표시를 한다.
[탐색 정점 : 정점 6]

정점 6과 인접한 정점은 모두 방문했기 때문에, 갱신할 정점이 존재하지 않는다.
정점 6을 탐색 했음으로 방문표시를 한다.
[탐색 정점 : 정점 3]
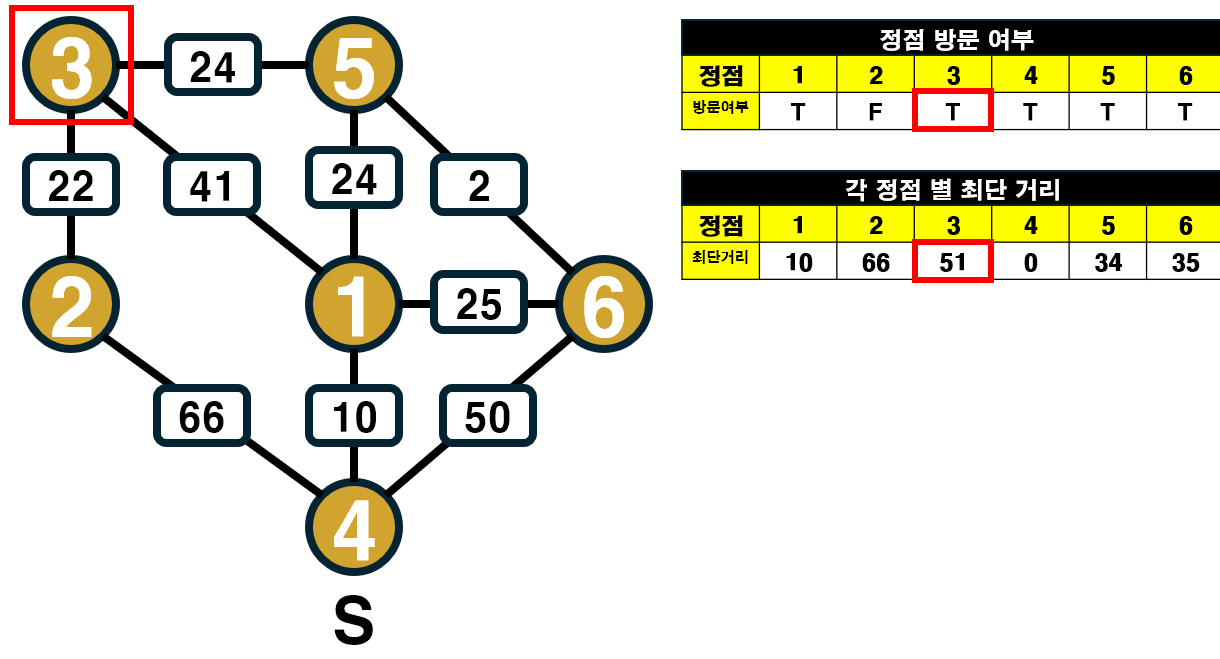
정점 3과 인접한 정점 중 방문하지 않은 정점은 정점 2 이다.
기존과 비교하여 최단 거리를 갱신한다.
정점 2 최단 거리 : 기존 거리 (66) > 새로운 거리 (51 + 22 = 73) 이므로, 최단 거리가 기존 거리로 유지된다.
정점 3을 탐색 했음으로 방문표시를 한다.
[탐색 정점 : 정점 2]

정점 2과 인접한 정점 중 방문하지 않은 정점 존재하지 않는다.
정점 2을 탐색 했음으로 방문표시를 한다.
[모든 정점 탐색 완료!]
모든 정점을 탐색했기 때문에, 시작점인 정점 4 부터 각 정점 별 최단 거리를 구하였다.
- Java 코드로 '다익스트라 알고리즘' 을 구현
//Node
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
class Node implements Comparable<Node> {
int index;
int cost;
public Node(int index, int cost) {
this.index = index;
this.cost = cost;
}
/*
* this.cost > o.cost : -1
* this.cost < o.cost : 1
* this.cost == o.cost : 0
*/
@Override
public int compareTo(Node o) {
return Integer.compare(this.cost, o.cost);
}
}
public class Dijkstra_Test {
static ArrayList<Node>[] graph;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
//그래프 초기화
graph = new ArrayList[7]; //1 ~ 6
for (int i = 0; i <= 6; i++) graph[i] = new ArrayList<>();
// 양방향 간선 추가
graph[4].add(new Node(1, 10));
graph[1].add(new Node(4, 10)); // 반대 방향
graph[3].add(new Node(5, 24));
graph[5].add(new Node(3, 24)); // 반대 방향
graph[5].add(new Node(6, 2));
graph[6].add(new Node(5, 2)); // 반대 방향
graph[3].add(new Node(1, 41));
graph[1].add(new Node(3, 41)); // 반대 방향
graph[5].add(new Node(1, 24));
graph[1].add(new Node(5, 24)); // 반대 방향
graph[4].add(new Node(6, 50));
graph[6].add(new Node(4, 50)); // 반대 방향
graph[2].add(new Node(4, 66));
graph[4].add(new Node(2, 66)); // 반대 방향
graph[2].add(new Node(3, 22));
graph[3].add(new Node(2, 22)); // 반대 방향
graph[1].add(new Node(6, 25));
graph[6].add(new Node(1, 25)); // 반대 방향
//정점 개수 : 6, 시작점 : 정점 4
int[] result = dijkstra(6, graph, 4);
for (int i = 1; i <= 6; i++) {
if (result[i] == Integer.MAX_VALUE) {
bw.write("INF "); // 도달할 수 없는 경우
} else {
bw.write(result[i] + " ");
}
}
bw.flush();
bw.close();
}
private static int[] dijkstra(int n, ArrayList<Node>[] graph, int start) {
int[] distance = new int[n + 1];
boolean[] visited = new boolean[n + 1];
Arrays.fill(distance, Integer.MAX_VALUE);
distance[start] = 0;
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.offer(new Node(start, 0));
while (!pq.isEmpty()) {
Node node = pq.poll();
int currentNode = node.index;
visited[currentNode] = true;
//인접한 노드 탐색
for (Node adjacentNode : graph[currentNode]) {
if (!visited[adjacentNode.index] && distance[adjacentNode.index] > distance[currentNode] + adjacentNode.cost) {
distance[adjacentNode.index] = distance[currentNode] + adjacentNode.cost;
pq.offer(new Node(adjacentNode.index, distance[adjacentNode.index]));
}
}
}
//10 66 51 0 34 35
return distance;
}
}
- 관련 PS 문제
https://notorious.tistory.com/370
[BOJ] BOJ_1753 최단경로 (JAVA)
[백준 1753번 최단경로]https://www.acmicpc.net/problem/1753[접근 방법]'그래프의 한 정점에서 모든 정점까지의 최단 거리를 구하는 알고리즘' 인 다익스트라 알고리즘 반복 학습을 위해 이 문제를 선택
notorious.tistory.com
https://notorious.tistory.com/369
[programmers] 합승 택시 요금 (JAVA)
[ 2021 KAKAO BLIND RECRUITMENT - 합승 택시 요금 ]https://school.programmers.co.kr/learn/courses/30/lessons/72413 프로그래머스코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로
notorious.tistory.com
'Algorithm' 카테고리의 다른 글
| 깊이/너비 우선탐색 (DFS / BFS) 알고리즘 / Java 코드 (0) | 2024.08.08 |
|---|---|
| "탐색 (Search)" 알고리즘에 대해 알아보자. (0) | 2023.02.03 |
| [알고리즘] Dynamic Programming (0) | 2022.06.06 |
